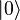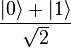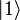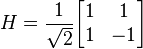I.                   Pendahuluan

Quantum Computation atau komputer kuantum adalah sebuah alat untuk perhitungan, dimana perhitungan ini menggunakan langsung fenomena kuantum mekanik dan perhitungan ini seperti superposisi dan belitan untuk melakukan operasi pada data. Perbedaan komputer kuantum dengan komputer klasik adalah pada sebuah komputer klasik memiliki memori terdiridari bit, dimana tiap bit mewakili salah satu atau nol. Sedangkan sebuah komputer kuantummempertahankan urutan qubit. Prinsip dasar komputer kuantum adalah bahwa sifat kuantum dari partikel dapat digunakan untuk mewakili data dan struktur data, dan bahwa mekanika kuantum dapat digunakan untuk melakukan operasi dengan data ini. Dalam hal ini untuk mengembangkan komputer dengan sistem kuantum diperlukan suatu logika baru yang sesuai dengan prinsip kuantum.

Pengoprasian Data Glubit

Pengoprasian Data Glubit

Secara umum komputer kuantum dengan qubit n bisa dalam superposisi sewenang-wenang hingga 2 n negara bagian yang berbeda secara bersamaan (ini dibandingkan dengan komputer normal yang hanya dapat di salah satu negara n 2 pada satu waktu). Komputer kuantum yang beroperasi dengan memanipulasi qubit dengan urutan tetap gerbang logika quantum. Urutan gerbang untuk diterapkan disebut algoritma quantum.

Sebuah contoh dari implementasi qubit untuk komputer kuantum bisa mulai dengan menggunakan partikel dengan dua putaran menyatakan: “down” dan “up”. Namun pada kenyataannya sistem yang memiliki suatu diamati dalam jumlah yang akan kekal dalam waktu evolusi dan seperti bahwa A memiliki setidaknya dua diskrit dan cukup spasi berturut-turut eigen.  Misalnya saat spin atom mengarah ke atas (up) kita beri lambang 1, sedangkan spin down adalah 0.

QUATUM GATES

QUATUM GATES

Gerbang kuantum

dari Wikipedia, ensiklopedia gratis

Untuk permainan, lihat Quantum Gate (video game).

Dalam komputasi kuantum dan khususnya sirkuit kuantum model komputasi, sebuah gerbangkuantum (quantum atau gerbang logika) adalah dasar sirkuit kuantum yang beroperasi pada sejumlah kecil qubit. Mereka adalah blok bangunan sirkuit kuantum, seperti klasik gerbang logikaadalah untuk sirkuit digital konvensional.
Tidak seperti banyak gerbang logika klasik, logika kuantum gerbang reversibel. Namun, adalah mungkin untuk melakukan komputasi klasik menggunakan gerbang hanya reversibel. Sebagai contoh, reversibel gerbang Toffoli dapat melaksanakan semua fungsi Boolean. Gerbang ini memiliki setara kuantum langsung, menunjukkan bahwa sirkuit kuantum dapat melakukan semua operasi yang dilakukan oleh sirkuit klasik.
Quantum gerbang logika yang diwakili oleh matriks kesatuan. Gerbang kuantum yang paling umum beroperasi pada ruang satu atau dua qubit, seperti umum klasik gerbang logika beroperasi pada satu atau dua bit. Ini berarti bahwa sebagai matriks, gerbang kuantum dapat dijelaskan oleh 2 × 2 atau 4 × 4 matriks kesatuan. 

Isi

• 1 gerbang Umumnya digunakan
  • 1.1 Hadamard gerbang
  • 1.2 Pauli-X gerbang
  • 1,3 Pauli-Y gerbang
  • 1.4 Pauli-Z gerbang
  • 1,5 Fase gerbang pergeseran
  • Gerbang 1,6 Swap
  • 1,7 Square root dari gerbang Swap
  • 1,8 gerbang Terkendali
  • 1,9 Toffoli gerbang
  • 1.10 Fredkin gerbang
• 2 gerbang kuantum Universal
• 3 Sejarah

Gerbang yang biasa digunakan

Gerbang kuantum biasanya direpresentasikan sebagai matriks. Sebuah gerbang yang bekerja pada k qubit diwakili oleh 2 ^k x 2 ^k matriks kesatuan. Jumlah qubit dalam input dan output dari gerbang harus sama. Tindakan gerbang kuantum ditemukan dengan mengalikan matriks mewakili gerbang dengan vektor yang mewakili keadaan kuantum. Berikut ini, representasi vektor dari qubit tunggal: 

 .

dan representasi vektor dari dua qubit adalah: 

 .

dimana  adalah negara di mana qubit pertama memiliki nilai dan yang kedua qubit b. 

Hadamard gerbang

Informasi lebih lanjut: Hadamard_transform § Quantum_computing_applications

The Hadamard gerbang bertindak pada qubit tunggal. Ini peta negara secara  untuk  dan  untuk  dan merupakan rotasi  tentang sumbu  . Hal ini diwakili oleh matriks Hadamard: 

Representasi rangkaian dari Hadamard gerbang

 .

Sejak  dimana I adalah matriks identitas, H memang matriks kesatuan. 

Pauli-X gerbang

Pauli-X gerbang bertindak pada qubit tunggal. Ini adalah setara kuantum dari gerbang NOT(sehubungan dengan dasar standar  .  , Yang hak Z -direction). Ini setara dengan rotasiBloch Sphere sekitar sumbu X dengan π radian. Ini peta  untuk  dan  untuk . Hal ini diwakili oleh Pauli matriks: 

 .

Pauli-Y gerbang

Pauli-Y gerbang bertindak pada qubit tunggal. Ini setara dengan rotasi di sekitar sumbu Y dari Bloch Sphere oleh radian π. Ini peta  untuk  dan  untuk  . Hal ini diwakili oleh Pauli matriks Y: 

 .

Pauli-Z gerbang

Pauli-Z gerbang bertindak pada qubit tunggal. Ini setara dengan rotasi di sekitar sumbu Z dari Bloch Sphere oleh radian π. Dengan demikian, itu adalah kasus khusus dari gerbang pergeseran fasa (berikutnya) dengan θ = π. Ia meninggalkan negara secara  tidak berubah dan peta untuk  . Hal ini diwakili oleh Pauli Z matriks: 

 .

Gerbang pergeseran fasa

Ini adalah sebuah keluarga tunggal qubit gerbang yang meninggalkan negara secara  tidak berubah dan peta  untuk  . Probabilitas mengukur  atau  tidak berubah setelah menerapkan gerbang ini, namun memodifikasi fase keadaan kuantum. Ini setara dengan menelusuri lingkaran horizontal (garis lintang) pada Bloch Sphere oleh  radian. 

di mana φ adalah pergeseran fasa. Beberapa contoh umum adalah  gerbang mana φ =  , Gerbang fase di mana φ =  dan gerbang Pauli-Z di mana φ = π. 

Gerbang Swap

Representasi rangkaian dari SWAP gerbang

Gerbang Swap swap dua qubit. Sehubungan dengan dasar  .  .  .  , Itu diwakili oleh matriks: 

 .

Akar kuadrat dari gerbang Swap

Representasi dari sirkuit  gerbang

Sqrt (swap) gerbang melakukan setengah-cara swap dua qubit. Ini adalah universal seperti bahwa setiap kuantum banyak qubit gerbang dapat dibangun dari hanya sqrt (swap) dan gerbang qubit tunggal. 

 .

Gerbang dikendalikan

Representasi sirkuit dikendalikan gerbang NOT

Gerbang dikendalikan bertindak atas 2 atau lebih qubit, di mana satu atau lebih qubit bertindak sebagai kontrol untuk beberapa operasi. Sebagai contoh, gerbang NOT dikendalikan (atau CNOT) bertindak atas 2 qubit, dan melakukan operasi TIDAK pada qubit kedua hanya ketika qubit pertama adalah  , Dan sebaliknya daun itu berubah. Hal ini diwakili oleh matriks 

 .

Secara umum jika U adalah gerbang yang beroperasi pada qubit tunggal dengan representasi matriks 

 .

maka-U dikontrol gerbang gerbang yang beroperasi pada dua qubit sedemikian rupa bahwa qubit pertama berfungsi sebagai kontrol. Ini peta negara secara sebagai berikut. 

Representasi rangkaian dari controlled- gerbang U

Matriks mewakili U dikendalikan 

 .

dikontrol X, Y dan Z gerbang

dikendalikan-X gerbang

dikendalikan-Y gerbang

dikendalikan-Z gerbang

Ketika U adalah salah satu matriks Pauli, σ _{x, y} σ, atau σ _z, istilah masing"X controlled-", "controlled- Y", atau"Z controlled-" kadang-kadang digunakan. ^[1] 

Toffoli gerbang

Artikel utama: Toffoli gerbang

Representasi rangkaian dari Toffoli gerbang

The Toffoli gerbang, juga CCNOT gerbang, adalah gerbang 3-bit, yang umum untuk perhitungan klasik. Kuantum Toffoli gerbang gerbang yang sama, ditetapkan untuk 3 qubit. Jika dua bit pertama adalah di negara bagian  , Itu menerapkan Pauli-X pada bit ketiga, yang lain itu tidak apa-apa.Ini adalah contoh dari gerbang dikendalikan. Karena merupakan analog kuantum gerbang klasik, itu benar-benar ditentukan oleh tabel kebenarannya. 

Tabel kebenaran	Bentuk matriks
MEMASUKKAN OUTPUT 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 1 0 0 1 0 0 1 0 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 0

Hal ini dapat juga digambarkan sebagai gerbang yang memetakan  untuk  . 

Fredkin gerbang

Artikel utama: gerbang Fredkin

Representasi rangkaian dari Fredkin gerbang

The Fredkin gerbang (juga CSWAP gerbang) adalah gerbang 3-bit yang melakukan dikendalikanpertukaran. Hal ini yang universal untuk perhitungan klasik. Ini memiliki properti yang berguna bahwa angka 0 dan 1 dilestarikan sepanjang, yang dalam model yang bola bilyar berarti jumlah yang sama dari bola adalah output sebagai input. 

Tabel kebenaran	Bentuk matriks
MEMASUKKAN OUTPUT C Saya 1 Saya I2 C O 1 O 2 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 1 0 0 1 0 0 1 0 1 1 1 0 1 1 0 1 0 1 1 1 1 1 1 1

Gerbang kuantum Universal

Informal, satu set gerbang kuantum universal setiap set gerbang yang operasi apapun yang mungkin terjadi pada komputer kuantum dapat dikurangi, yaitu, setiap operasi kesatuan lain dapat dinyatakan sebagai urutan terbatas gerbang dari set. Secara teknis, hal ini tidak mungkin karena jumlah gerbang kuantum yang mungkin adalah terhitung, sedangkan jumlah urutan terbatas dari satu set yang terbatas adalah dihitung. Untuk mengatasi masalah ini, kita hanya mengharuskan operasi kuantum apapun dapat didekati dengan urutan gerbang dari himpunan berhingga ini. Selain itu, untuk kasus tertentu qubit tunggal unitaries yang Teorema Solovay-Kitaev menjamin bahwa hal ini dapat dilakukan secara efisien.
Satu set sederhana dari dua qubit gerbang kuantum universal gerbang Hadamard (  ), Yang  gerbang  , Dan gerbang NOT dikendalikan.
Sebuah single-gerbang set gerbang kuantum universal yang juga dapat dirumuskan dengan menggunakan tiga qubit Deutsch gerbang  , Yang melakukan transformasi ^[2] 

Universal klasik gerbang logika, yang Toffoli gerbang, direduksi menjadi gerbang Deutsch, , Sehingga menunjukkan bahwa semua operasi logika klasik dapat dilakukan pada sebuah komputer kuantum universal. 

Sejarah

Notasi saat gerbang kuantum dikembangkan oleh Barenco et al., ^[3] bangunan di notasi diperkenalkan oleh Feynman. ^[