QUATUM GATES
Gerbang kuantum
dari Wikipedia, ensiklopedia gratis
Untuk permainan, lihat Quantum Gate (video game).
Dalam komputasi kuantum dan khususnya sirkuit kuantum model komputasi, sebuah gerbangkuantum (quantum atau gerbang logika) adalah dasar sirkuit kuantum yang beroperasi pada sejumlah kecil qubit. Mereka adalah blok bangunan sirkuit kuantum, seperti klasik gerbang logikaadalah untuk sirkuit digital konvensional.Tidak seperti banyak gerbang logika klasik, logika kuantum gerbang reversibel. Namun, adalah mungkin untuk melakukan komputasi klasik menggunakan gerbang hanya reversibel. Sebagai contoh, reversibel gerbang Toffoli dapat melaksanakan semua fungsi Boolean. Gerbang ini memiliki setara kuantum langsung, menunjukkan bahwa sirkuit kuantum dapat melakukan semua operasi yang dilakukan oleh sirkuit klasik.
Quantum gerbang logika yang diwakili oleh matriks kesatuan. Gerbang kuantum yang paling umum beroperasi pada ruang satu atau dua qubit, seperti umum klasik gerbang logika beroperasi pada satu atau dua bit. Ini berarti bahwa sebagai matriks, gerbang kuantum dapat dijelaskan oleh 2 × 2 atau 4 × 4 matriks kesatuan.
Isi
Gerbang yang biasa digunakan
Gerbang kuantum biasanya direpresentasikan sebagai matriks. Sebuah gerbang yang bekerja pada k qubit diwakili oleh 2 k x 2 k matriks kesatuan. Jumlah qubit dalam input dan output dari gerbang harus sama. Tindakan gerbang kuantum ditemukan dengan mengalikan matriks mewakili gerbang dengan vektor yang mewakili keadaan kuantum. Berikut ini, representasi vektor dari qubit tunggal:
 .
.
 .
.
 adalah negara di mana qubit pertama memiliki nilai dan yang kedua qubit b.
adalah negara di mana qubit pertama memiliki nilai dan yang kedua qubit b. Hadamard gerbang
Informasi lebih lanjut: Hadamard_transform § Quantum_computing_applications
The Hadamard gerbang bertindak pada qubit tunggal. Ini peta negara secara 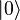 untuk
untuk 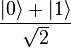 dan
dan 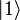 untuk
untuk  dan merupakan rotasi
dan merupakan rotasi  tentang sumbu
tentang sumbu  . Hal ini diwakili oleh matriks Hadamard:
. Hal ini diwakili oleh matriks Hadamard:
Representasi rangkaian dari Hadamard gerbang
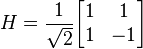 .
.
 dimana I adalah matriks identitas, H memang matriks kesatuan.
dimana I adalah matriks identitas, H memang matriks kesatuan. Pauli-X gerbang
Pauli-X gerbang bertindak pada qubit tunggal. Ini adalah setara kuantum dari gerbang NOT(sehubungan dengan dasar standar
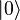 .
. 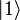 , Yang hak Z -direction). Ini setara dengan rotasiBloch Sphere sekitar sumbu X dengan π radian. Ini peta
, Yang hak Z -direction). Ini setara dengan rotasiBloch Sphere sekitar sumbu X dengan π radian. Ini peta 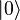 untuk
untuk 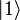 dan
dan 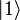 untuk
untuk 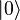 . Hal ini diwakili oleh Pauli matriks:
. Hal ini diwakili oleh Pauli matriks:
 .
.
Pauli-Y gerbang
Pauli-Y gerbang bertindak pada qubit tunggal. Ini setara dengan rotasi di sekitar sumbu Y dari Bloch Sphere oleh radian π. Ini peta
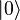 untuk
untuk 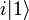 dan
dan 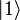 untuk
untuk  . Hal ini diwakili oleh Pauli matriks Y:
. Hal ini diwakili oleh Pauli matriks Y:
 .
.
Pauli-Z gerbang
Pauli-Z gerbang bertindak pada qubit tunggal. Ini setara dengan rotasi di sekitar sumbu Z dari Bloch Sphere oleh radian π. Dengan demikian, itu adalah kasus khusus dari gerbang pergeseran fasa (berikutnya) dengan θ = π. Ia meninggalkan negara secara
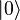 tidak berubah dan peta
tidak berubah dan peta 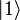 untuk
untuk  . Hal ini diwakili oleh Pauli Z matriks:
. Hal ini diwakili oleh Pauli Z matriks:
 .
.
Gerbang pergeseran fasa
Ini adalah sebuah keluarga tunggal qubit gerbang yang meninggalkan negara secara
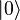 tidak berubah dan peta
tidak berubah dan peta 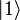 untuk
untuk  . Probabilitas mengukur
. Probabilitas mengukur 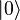 atau
atau 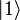 tidak berubah setelah menerapkan gerbang ini, namun memodifikasi fase keadaan kuantum. Ini setara dengan menelusuri lingkaran horizontal (garis lintang) pada Bloch Sphere oleh
tidak berubah setelah menerapkan gerbang ini, namun memodifikasi fase keadaan kuantum. Ini setara dengan menelusuri lingkaran horizontal (garis lintang) pada Bloch Sphere oleh  radian.
radian.
 gerbang mana φ =
gerbang mana φ =  , Gerbang fase di mana φ =
, Gerbang fase di mana φ =  dan gerbang Pauli-Z di mana φ = π.
dan gerbang Pauli-Z di mana φ = π. Gerbang Swap
Representasi rangkaian dari SWAP gerbang
 .
.  .
.  .
.  , Itu diwakili oleh matriks:
, Itu diwakili oleh matriks:
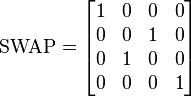 .
.
Akar kuadrat dari gerbang Swap
Representasi dari sirkuit  gerbang
gerbang
 gerbang
gerbang .
.
Gerbang dikendalikan
Representasi sirkuit dikendalikan gerbang NOT
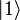 , Dan sebaliknya daun itu berubah. Hal ini diwakili oleh matriks
, Dan sebaliknya daun itu berubah. Hal ini diwakili oleh matriks
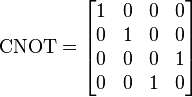 .
.
 .
.
Representasi rangkaian dari controlled- gerbang U
 .
.
Toffoli gerbang
Artikel utama: Toffoli gerbang
Representasi rangkaian dari Toffoli gerbang
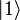 , Itu menerapkan Pauli-X pada bit ketiga, yang lain itu tidak apa-apa.Ini adalah contoh dari gerbang dikendalikan. Karena merupakan analog kuantum gerbang klasik, itu benar-benar ditentukan oleh tabel kebenarannya.
, Itu menerapkan Pauli-X pada bit ketiga, yang lain itu tidak apa-apa.Ini adalah contoh dari gerbang dikendalikan. Karena merupakan analog kuantum gerbang klasik, itu benar-benar ditentukan oleh tabel kebenarannya. | Tabel kebenaran | Bentuk matriks | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 untuk
untuk  .
. Fredkin gerbang
Artikel utama: gerbang Fredkin
Representasi rangkaian dari Fredkin gerbang
| Tabel kebenaran | Bentuk matriks | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Gerbang kuantum Universal
Informal, satu set gerbang kuantum universal setiap set gerbang yang operasi apapun yang mungkin terjadi pada komputer kuantum dapat dikurangi, yaitu, setiap operasi kesatuan lain dapat dinyatakan sebagai urutan terbatas gerbang dari set. Secara teknis, hal ini tidak mungkin karena jumlah gerbang kuantum yang mungkin adalah terhitung, sedangkan jumlah urutan terbatas dari satu set yang terbatas adalah dihitung. Untuk mengatasi masalah ini, kita hanya mengharuskan operasi kuantum apapun dapat didekati dengan urutan gerbang dari himpunan berhingga ini. Selain itu, untuk kasus tertentu qubit tunggal unitaries yang Teorema Solovay-Kitaev menjamin bahwa hal ini dapat dilakukan secara efisien.
Satu set sederhana dari dua qubit gerbang kuantum universal gerbang Hadamard (
 ), Yang
), Yang  gerbang
gerbang  , Dan gerbang NOT dikendalikan.
, Dan gerbang NOT dikendalikan.Sebuah single-gerbang set gerbang kuantum universal yang juga dapat dirumuskan dengan menggunakan tiga qubit Deutsch gerbang
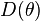 , Yang melakukan transformasi [2]
, Yang melakukan transformasi [2]
 , Sehingga menunjukkan bahwa semua operasi logika klasik dapat dilakukan pada sebuah komputer kuantum universal.
, Sehingga menunjukkan bahwa semua operasi logika klasik dapat dilakukan pada sebuah komputer kuantum universal. 








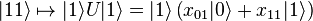






Tidak ada komentar:
Posting Komentar